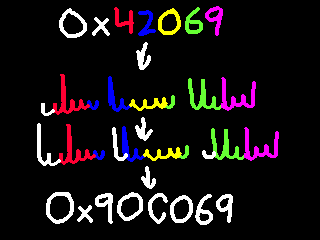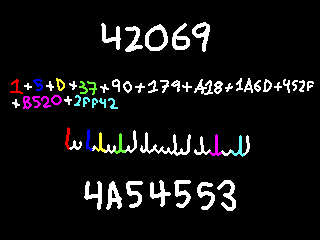well, i happen to be a sizecoder, which means, among other things, i try to write programs under intensely limited byte counts or character counts. i'm also fascinated by minimalistic languages. in the past, this used to primarily be lisp: you can implement the core language in just 33 lines by 60 columns of c78:
#include<stdio.h>
#define NEW calloc(1, sizeof(V))
#define EI else if
typedef struct V{struct V*a,*d;}V;P(V*p){if(p->d)printf("(")
,P(p->a),printf(" . "),P(p->d),printf(")");else printf("%s",
p->a);}V*R(){int c;char*p;V*o=NEW,*q=o;if((c=getchar())<0)r\
eturn 0;switch(c){case';':while((c=getchar())>0&&c!='\n');c\
ase' ':case'\n':return R();case'\'':(o->a=NEW)->a="quote";(o
->d=NEW)->a=R();(o->d->d=NEW)->a="nil";return o;case'(':whi\
le(q->a=R())q=q->d=NEW;q->a="nil";return o;case')':return 0;
}o->a=p=malloc(32);o->d=0;do*p++=c;while((c=getchar())>0&&!\
strchr("; \n'()",c));ungetc(c,stdin);*p=0;return o;}V*L(char
*s,V*e){return e->d?strcmp(e->a->a->a,s)?L(s,e->d):e->a->d:0
;}V*BV(c){V*v;(v=NEW)->a=c?"t":"nil";return v;}VB(V*v){retu\
rn!v->d&&!strcmp(v->a,"t");}V G={"nil"};V*E(V*p,V*e){V*v,*w,
*x,*y,z;if(!p->d)return L(p->a,e);if(p->a->d){int M=0;if(!s\
trcmp(p->a->a->a,"lambda")||(M=!strcmp(p->a->a->a,"macro")))
{v=p->a->d->a;w=p->d;x=e;while(v->d&&w->d){(y=NEW)->d=x;(y->
a=NEW)->a=v->a;y->a->d=M?w->a:E(w->a,e);v=v->d,w=w->d,x=y;}v
=E(p->a->d->d->a,x);return M?E(v,e):v;}}EI(!strcmp(p->a->a,\
"quote"))v=p->d->a;EI(!strcmp(p->a->a,"cons")){(v=NEW)->a=E(
p->d->a,e);v->d=E(p->d->d->a,e);}EI(!strcmp(p->a->a,"atom"))
v=BV(!E(p->d->a,e)->d);EI(!strcmp(p->a->a,"car"))v=E(p->d->a
,e)->a;EI(!strcmp(p->a->a,"cdr"))v=E(p->d->a,e)->d;EI(!strc\
mp(p->a->a,"eq"))x=E(p->d->a,e),w=E(p->d->d->a,e),v=BV(!x->d
&&!w->d&&!strcmp(x->a,w->a));EI(!strcmp(p->a->a,"cond")){for
(p=p->d;p->d;p=p->d)if(VB(E(p->a->a,e)))return E(p->a->d->a,
e);(v=NEW)->a="nil";}EI(!strcmp(p->a->a,"set"))z.d=memcpy(N\
EW,&G,sizeof(V)),(z.a=NEW)->a=p->d->a,v=z.a->d=E(p->d->d->a,
e),G=z;EI(!strcmp(p->a->a,"label"))(w=NEW)->d=e,(w->a=NEW)->
a=p->d->a,w->a->d=p,v=E(p->d->d->a,w);else(w=NEW)->a=E(p->a,
e),w->d=p->d,v=E(w,e);return v;}main(){V*x;while(printf("> "
),fflush(0),x=R())P(E(x,&G)),printf("\n");}
that's an entire interpreter. it even goes a
bit farther than just implementing enough to selfhost:
it has macros, too.
T[4096],c,t,x;char C[4096];main(){gets(C);do{for(;;)switch(C
[c++]){case 0:goto X;case'+':T[t]=T[t]+1&255;break;case'>':\
if(++t==4096)t=0;break;case'.':if(T[t])putchar(T[t]);else T[
t]=getchar()&255;break;case'[':if(!T[t]){x=1;while(x)x+=(C[c
]=='[')-(C[c]==']'),++c;}break;}X:c=0;}while(T[t]);}
this has a good chance of not compiling on your
machine because it uses the extremely evil
gets() function. when a manpage
has this as it's first line:
Never use this function.you know it's bad.
sure! one of the contendors for smallest possible
implementation is
forth.
precisely explaining the intricacies and idioms of
forth is out of the scope of this
document[0],
but do know that it has
a lot of intricacies.
anyway what matters is that it turns out the
language is very simple. and when i say very simple i
mean absurdly simple. i mean
430-bytes-simple. for context,
sectorlisp costs a whopping 96 bytes more.
i mean this simple:
000: ea bc 77 50 00 01 40 5f ff 35 eb 53 03 77 01 21
010: 5f 8f 05 eb 4a 0c 77 03 73 70 40 54 eb 41 15 77
020: 03 72 70 40 52 eb 38 1e 77 02 30 23 58 f7 d8 19
030: c0 eb 17 27 77 01 2b 5f 58 01 f8 eb 0d 33 77 04
040: 6e 61 6e 64 5f 58 21 f8 f7 d0 50 eb 12 3d 77 04
050: 65 78 69 74 87 d4 5e eb 33 4d 77 02 73 40 53 ad
060: ff e0 59 77 01 3a e8 b4 00 56 89 fe 8b 47 06 89
070: c7 87 47 04 ab 88 c8 aa f3 a4 5e 88 0f b8 ff 26
080: ab b8 90 77 eb 30 87 d4 56 96 ad ad 87 d4 eb cf
090: 86 77 62 77 03 6b 65 79 91 cd 16 eb ad 92 77 04
0a0: 65 6d 69 74 58 e8 94 00 eb b5 9d 77 81 3b 88 0f
0b0: b8 54 77 8b 7f 06 ab 89 7f 06 eb a3 0e 0e 0e 1f
0c0: 07 17 bb 00 10 c7 47 04 aa 77 c7 47 06 00 79 bc
0d0: 02 00 b0 0d e8 65 00 ba 00 77 31 f6 56 46 89 37
0e0: e8 3a 00 8d 6f 04 89 ee ad 95 84 e4 74 e1 ac 50
0f0: 24 1f 38 c8 58 75 ef 51 57 f3 a6 5f 59 75 e7 24
100: 80 0a 07 96 be 36 78 74 aa ff e0 aa 3d 31 ff e8
110: 26 00 21 7f 02 3c 0a 75 f2 b8 20 00 ab 8b 7f 02
120: b0 20 38 1d 74 e7 ae 74 f9 31 c9 41 ae 75 fc 4f
130: 89 7f 02 29 cf c3 e0 77 31 c0 cd 16 b4 0e 3d b0
140: 0a cd 10 3c 0d 74 f8 c3
that's not even the code. that's a hexdump
of the code. lisp is tiny, but forth is even tinier.
there are three things that make forth weird an
unintuitive if you aren't used to it: it's
stack-based, the syntax is "split by whitespace",
and threading. (no not
that[1]
one (the
other[2]
one))
stack based means that there is one "data stack",
where operations pop their values off the data stack,
and push their results back onto the stack. instead of
1 + 2, it's
push(1) push(2) +.
it's "split by whitespace" syntax, meaning there are
no special keywords or operators (like lisp!).
everything is a
procedure[3].
and finally, it's threaded, which means forth code is
composed entirely of calls to procedures. at least,
semantically. in practice, they get inlined pretty
often, and sometimes straight up optimized out, but
it doesn't change the behaviour of the program. take
the following code:
: twice ( u -- u' ) dup + ;
: name ... ; is how forth defines a new
procedure. it's like name(){ ... } in c.
so this defines a new procedure named
twice. ( u -- u' ) here is
a comment that means "takes in an unsigned integer
[u] and gives back [--] a
changed version of it [u']". next, it is
defined as dup +, which duplicates the
integer [dup], adds it to the new copy
[+], then returns it [implicit].
twice(u) { return u + u; }
in c.
because a forth procedure is just defined in terms of other procedures, there's no need to store things like variable names, function signatures, or even instructions to call the procedures themselves. one only needs to store a series of pointers to each procedure in the definition, like so:
dup() { ... }
plus() { ... }
exit() { ... }
(*twice[3])() = {
&dup,
&plus,
&exit
};
that declaration is a bit hard to read. "array of 3
function pointers".
exit here is effectively forth's
return. it's automatically added at the
end of any definition, but it can also be put in the
middle to do an early return.
&exit, then
stop.
execute((**proc)()) {
while (*proc != &exit) {
(*proc)();
}
}
that's a bit awkward (why not just replace &exit
with a null pointer?) but there's a very good reason
for it being there: this isn't how threaded code
is typically implemented.
what we just discussed in fact has a name, and it's called direct threading. each pointer directly points to a procedure. however, our implementation if it is not without problems.
how do you push constants to the stack? the following code needs to compile somehow:
: add-two ( u -- u' ) 2 + ;
where 2 pushes two to the data stack. the
issue is, we can't just jam a number into the list of
pointers, because otherwise we'd try to call it as a
procedure.
lit, which reads the
next part of the definition as if it was a number
instead of a pointer, and push it to the stack.
lit() { ... }
(*add_two[4])() = {
&lit,
2,
&plus,
&exit
};
not so fast.
lit here, because it is impossible to
implement in c. our execute function
keeps track of which procedure we're currently
executing using a local variable. a local variable
that is inaccessible from lit.
here's the trick: every procedure ends with a bit of code that loads the next procedure and invokes it.
(**ip)();
stack[1024], *dsp = stack;
return_stack[1024], *rsp = return_stack;
dup() { ++dsp; dsp[-1] = dsp[-2]; (*ip++)(); }
plus() { --dsp; dsp[-1] += *dsp; (*ip++)(); }
exit() { ip = *--rsp; (*ip++)(); }
lit() { ++dsp; dsp[-1] = *ip++; (*ip++)(); }
execute((**proc)()) { ip = proc; (*ip++)(); }
now it works.
exit more
clear: there is no definite "end" of a procedure, we
just happen to have a procedure that "returns".
execute.
setjmp-longjmp, but this is
besides the point of forth.
with indirect threading, you don't store pointers to
the procedure, but a pointer to a
pointer to a procedure. this probably seems
useless, but it has a few benefits. for one: calling
forth procedures from other forth procedures is now
significantly less painful to deal with. take that
twice procedure from earlier. say we
want to use it for a thrice procedure.
: thrice dup twice + ;
how do we actually compile this. we can't put the
address of the definition of twice
because twice isn't a function itself,
it's an array of function pointers. so, we have to use
another hack!
call() { *rsp++ = ip + 1; ip = *ip; (**ip++)(); }
(*thrice[5])() = {
&dup,
&call,
&twice,
&add,
&exit
};
this stacks up. very. very fast.
&call is stored. instead of it being
stored every procedure invocation, it's stored
every procedure definition, as the first
pointer.
(***ip)();[4]
/* docol here likely stands for DO COLon definition */
/* because forth procedures are defined with colons */
docol() { *rsp++ = ip; ip = ip[-1] + 1; (**ip++)(); }
execute((***proc)()) { ip = proc; (**ip++)(); }
(*dup_i)() = &dup;
(*plus_i)() = +
(*exit_i)() = &exit;
(**twice[4])() = {
&docol,
&dup_i,
&plus_i,
&exit_i
};
this makes more sense, because programmers tend to
define procedures less often than they use them. for a
procedure that is used a single time, this saves no
memory. but every additional time it is referenced,
it saves one pointer.
let's put some numbers onto this. here's a very very simple example program:
: twice dup + ;
: foo 21 twice . bye
we're going to assume that the
only[5]
procedures defined beforehand are:
dup+lit (for 21).
(which is printf("%d",x))exit (for ;)bye
(which is exit(0))
int and void * are the same
size, which makes my life easier.
(**twice[4])() = {
&docol,
&dup_i,
&plus_i,
&exit_i
};
(**foo[6])() = {
&docol,
&lit_i,
21,
&twice,
&print_i,
&bye_i
};
i count 10 pointers. 10 pointers × 4 bytes per
pointer × 8 bits per byte = 320 bits. nice!
there's a simple and pretty low hanging fruit size optimization that can be done here. instead of referring to procedures by pointer, one can keep a table of pointers and then only store the indicies.
dup_i[2], plus_i[2], lit_i[2],
print_i[2], bye_i[2], exit_i[2],
docode();
twice[4], foo[6];
(*table[7]) = {
&docol,
&docode,
&lit_i,
&plus_i,
&print_i,
&dup_i,
&exit_i,
&bye_i,
&twice,
&foo
};
/* this way, we only have to have */
/* a single token for "procedure */
/* implemented in c", instead of */
/* having one token per procedure */
docode() {
((int(*)()) table[ip[-1]][1])();
((int(*)()) table[*table[*ip++]])();
}
dup_i[2] = { 1, &dup };
plus_i[2] = { 1, &plus };
lit_i[2] = { 1, &lit };
print_i[2] = { 1, &print };
byte_i[2] = { 1, &byte };
exit_i[2] = { 1, &exit };
twice[4] = {
0, /* docol */
5, /* dup */
3, /* + */
6 /* exit */
};
foo[6] = {
0, /* docol */
2, /* lit */
21,
8, /* twice */
4, /* . */
7 /* bye */
};
funnily enough, because our pointers are the same size
as our integers, this actaully doesn't change the size
of the code. (in fact, it makes it bigger, because now
there's a whole table being stored alongside it.)
next, and we'll do
that in a moment.
i was using
marginalia search
to find more pages and resources related to forth, and
eventually stumbled upon a very strange github
repository called
nibbleforth.
nibbleforth tries to strike a balance between size and
speed efficiency, but leaning heavily toward size.
unfortunately, many of the links on that repository
have suffered 12 years of link rot, so most of them
are dead.
the ideas there are still very readable and equally as
interesting. but, again, nibbleforth tries to
balance speed and efficiency. which is not
what we're trying to do, our goal is to optimize for
size, by any means necessary.
there are two major features at play with nibbleforth:
hexarian varint tokens, which means that the most
common procedures get 4-bit encodings (hence,
nibbleforth); and using a dictionary coder to
effectively refactor code automatically, because
programmers are not always optimal with how they
factor their own code. and they shouldn't have to be!
the programmer's job is to write code that is readable
for humans first, and efficient for computers second.
back to token threading, let's look at
more commonly known as 16-bit.
encoding everything as a short does in fact save
space. to be more precise, it halves the space
required. so now we're looking at 160 bits. the
cost is that now we're limited to just 65536
procedures. but, well, that's the amount of memory
that some systems had in bytes, let alone entire
procedures. so, we're probably fine.
still, it'd be ideal to not have such a low limit.
short *ip;
(*table)[65536];
token;
next() {
token = *ip++;
table[token]();
}
more commonly known as 8-bit.
this happens to be borderline esoteric. only 256
procedures is not a lot of procedures. still, this
rehalves the amount of memory required down to just
80 bits.
char *ip;
(*table)[256];
token;
next() {
token = *ip++;
table[token]();
}
more commonly known as 4-bit.
this is Actually esoteric. 16 procedures. just barely
fits. 40 bits.
there's no easy way to code this without manually
pointing your pointers. and i'm too lazy. so. this is
your chance to exercise your c knowledge! wahoo! okay
i'm out of breath just from that.
more commonly known as 3-bit.
this just Barely fits the test. 30 bits. cons:
next is now very hard to write, because
not only do you have to point to sub-char bit
groupings, but sometimes the groups span across
different consequetive bytes, and you have to stitch
it back together again.
it does in fact fit inside of a single integer now,
though. which is funny.
here's a variable width encoding. the idea is simple:
split up the number you want to encode into septet
chunks. every chunk except the last one gets a 1 as
its most significant bit, the last one gets a 0 to
indicate that the number is complete.
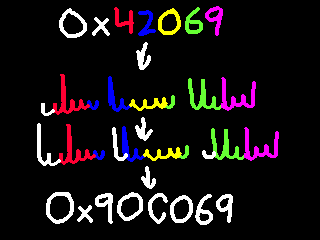
this is fairly easy and efficient to implement,
because everything's byte-aligned.
char *ip;
(*table)[1024]; /* this can be arbitrarily large */
token;
next() {
token = 0;
while (*ip & 0x80) {
token <<= 7;
token |= *ip & 0x7F;
++ip;
}
token <<= 7;
token |= *ip & 0x7F;
table[token]();
}
because we don't have more than 128 procedures, this
is equivalent to a tesserhexian fixed-width encoding
for our sample program. so, it is, in fact, still 80
bits.
this is the one nibbleforth uses! it's identical to
tesserhexian varint, except instead of octets, we
split the number into quatertets. i.e. nibbles.
because we don't have more than 8
procedures, this is equivalent to hexarian
fixed-width. i.e. 40 bits.
fibonacci coding is a very elegant (and very
efficient) universal code, meaning it's an effective
way to store any positive integer. as implied by the
name, this encoding uses fibonacci numbers.
specifically, each bit from left to right corresponds
to a fibonacci number, two ones in a row indicate the
end of a number, and then you sum up all the fibonacci
numbers corresponding to the one bits.
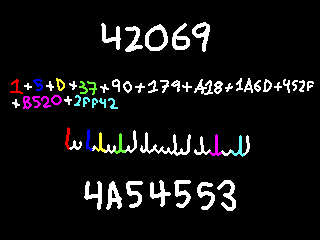
proving that two consequetive one bits can't occur in
the middle of a number is a very fun challenge.
fibonacci coding happens to be very efficient at
encoding small positive integers, at the cost of
being incredibly unwieldy to actually implement.
nonetheless, it is an option.
what makes it a poor choice is that, using
conventional token threading, it actually makes
assigns the longest codes to user defined
procedures. which is not good. most of a program
is taken up by user defined procedures. it would be
better if the user defined procedures had shorter code
than the system-defined ones did.
11 > 1 DOCOL
10011 > 6 DUP
1011 > 4 +
01011 > 7 EXIT
11 > 1 DOCOL
0011 > 3 LIT
10000011 > 22 21
100011 > 9 TWICE
00011 > 5 .
000011 > 8 BYE
11100111 01101011 11001110 00001110
00110001 1000011
47 bits, arbitrary number of procedures.
in most forth programs, other than stack shuffling,
most of the procedures refer back to very recently
defined procedures. we can exploit this by giving the
most recent procedures shorter encodings than the
procedures defined farther in the past. and because
forth procedures can't actually be
recursive[6],
we can assign the token 1 to the
procedure directly before the one being defined, the
token 2 to the procedure before that, et
cetera.
: foo ... ;
: bar ... ;
: baz ... ;
: qux foo bar baz ;
( 3 2 1 )
i'm too lazy to implement this too so wow!!! so many
reader exercises!!! hahahahahaha!!!!!
we've already seen two "doer"s: docol and
docode. doers effectively control what
language the procedure is defined in. however, forth
allows you to define your own language on top of it,
and along with that, you can write your own doers
using a very brain melting procedure called
does>[7].
however, the most common doer is going to be docol,
since that's the one that handles procedures that are
written in forth, instead of machine code or some
higher level domain specific language. so, we can give
docol a 1-bit code, and docode and dodoes 2-bit codes,
like this:
0 - docol
10 - docode
11 - dodoes (essentially "other token")
that saves us an additional token per definition. the
best part is, that one tends to be the
longest token in the definition, too. because
docol, docode, and
dodoes are going to be the first three
procedures in the table.
0 > 0 DOCOL
0011 > 3 DUP
00011 > 5 +
011 > 2 EXIT
0 > 0 DOCOL
01011 > 7 LIT
10000011 > 22 21
11 > 1 TWICE
00011 > 5 .
011 > 2 BYE
00011000 11011001 01110000 01111000
11011
37 bits.
the previous methods all hinged on one assumption: we don't compile the entire forth program all at once. for a traditional forth interpreter, this is in fact the case. however, if we're willing to bend the rules slightly, we can achieve not just a good token format, but the best token format.
nibbleforth happened to mention this, and it's a game
changer. (no not tha-)
if we know how many uses a procedure has ahead of
time, we can assign shorter tokens to the most used
ones, and longer tokens to the least used ones. the
previous approaches all made assumptions on which
procedures are used the most often, but if we have
the whole file to read at once, we can make
optimal assumptions.
huffman coding is an algorithm that, given a set of
symbols and their frequencies, works out a prefix-free
binary code for them. prefix-free means that if you
read a set of bits that correspond to a symbol, you
can't get a different symbol by reading more bits.
in this case, our symbols are the procedures, and
their frequencies can be analyzed.
specifically, it generates a binary tree, where one
branch is followed if a zero bit is read, and the
other branch is followed if a one bit is read.
there's a critical part of the program we haven't been measuring, and congratulations if you've spotted it. it's the fact that the table actually also gets bigger as the program gets bigger. simply not measuring the table yields incorrect results. so, we have to go back through those approaches again.
yeah, i realize how weird that sounds, but bare with
me.
forth is a. very weird language. it's sort of like a
compiler with handlebars on it. it acts like a
compiler in some aspects, like an interpreter in
others, but not quite like a just in time compiler.
it's an interactive system, so the system needs to
not only compile all the procedures you define, but
also keep track of their names, so you can refer back
to them later.
the canonical way to do this is a bunch of dictionary
entries, where each entry has a pointer to the
previous entry, the name of the procedure, and then
the definition of the procedure. effectively, a linked
list.
we can, in fact, take some inspiration from this
dictionary system to make relative token threading
even more overpowered. instead of storing a table of
pointers, each procedure just points to the procedure
before it. then, we read a token, follow that many
procedures back, and then execute it. simple!
this cuts down our 282 bits into 282 bits and did i
say cuts down i meant keeps. the
reason this didn't change at all is because we're
still storing one pointer per procedure, so it's still
just a table, but the table entries are now spread
out through memory instead of being consecutive.
so, what we'd really like now is a way to somehow make
pointers smaller.
more precisely, self-relative pointers. what this means is that, instead of storing the memory address of a value, we store how far that memory address is from the pointer itself.
*dereference(*ptr) {
return (char *) ptr + *ptr;
}
this means that we can actually use fewer bits for the
pointer, which saves memory. however, this is only
feasible if the pointers are referring to relatively
close sections of memory. for a linked list, this is
definitely the case, and it means the values tend to
be smaller.
this requires no explanation.
well, nearly none. we're not going to point into the
middle of a byte, because as it turns out, the padding
required to get procedure definitions to align to byte
boundaries costs less than the three extra bits that
have to be stored per pointer.
001011 > 11 LINK
0 > 0 DOCOL
0011 > 3 DUP
00011 > 5 +
011 > 2 EXIT
00000 [padding]
00011 > 3 LINK
0 > 0 DOCOL
01011 > 7 LIT
10000011 > 22 21
11 > 1 TWICE
00011 > 5 .
011 > 2 BYE
00101100 01100011 01100000 00011001
01110000 01111000 11011
53 bits. that's impossibly small.
do the same trick as in fibonacci threading. where we
store a fibonacci pointer based linked list. we're
going to have to store a bit more information now,
though, because huffman coding generates a tree, we
need to somehow encode the information about where the
procedure is located inside the tree.
one technique comes to mind:
here's a set of procedures sorted by frequency:
18341 0
7620 dup
7551 ,
6189 +
4575 constant
4539 1
4443 swap
4241 and
4240 drop
4002 value
3976 exit
3364 2
3231 cr
3192 4
3173 @
2955 0=
2746 -
2733 true
2675 over
2669 or
we can construct a huffman tree that looks like this:
00000 swap
00001 and
00010 drop
00011 value
0010 dup
0011 ,
01000 2
01001 exit
01010 4
01011 cr
0110 +
01110 0=
01111 @
10000 true
10001 -
10010 over
10011 or
1010 constant
1011 1
11 0
where the left column is the actual token, and the
right column is the name of the procedure. we can then
resort it by frequency:
11 0
0010 dup
0011 ,
0110 +
1010 constant
1011 1
00000 swap
00001 and
00010 drop
00011 value
01001 exit
01000 2
01011 cr
01010 4
01111 @
01110 0=
10001 -
10000 true
10010 over
10011 or
now it's more apparent that the most common procedure,
0, which pushes a zero onto the stack,
has the shortest code of all of them, just two bits.
but the longer procedures have increasingly longer
codes the less frequently they're used.
__ 0
____ dup
____ ,
____ +
____ constant
____ 1
_____ swap
_____ and
_____ drop
_____ value
_____ exit
_____ 2
_____ cr
_____ 4
_____ @
_____ 0=
_____ -
_____ true
_____ over
_____ or
we can generate canonical codes for each procedure
based soley on their lengths by assigning a string of
zero bits to the most common procedure, then, to get
the token of the next procedure, we increment the
token of the last one, and then pad with zeroes until
we reach the length specified.
00 0
0100 dup
0101 ,
0110 +
0111 constant
1000 1
10010 swap
10011 and
10100 drop
10101 value
10110 exit
10111 2
11000 cr
11001 4
11010 @
11011 0=
11100 -
11101 true
11110 over
11111 or
proving that this always works no matter the frequency
data is a very fun exercise. the reason this works is
because huffman trees are always binary
trees.
2 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
we can then apply delta encoding to this. which means
that instead of storing each element individually, we
store the first element, and then the differences of
each element to the previous one.
2 2 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
this happens to make most of the elements zeroes,
and the nonzero elements very small. in fact, most of
the time those elements are either 0 or 1. so, we can
use an encoding that optimizes for inputs that are
mostly zeroes. one very simple solution is unary
coding, which means that to store a number, we store
that many one bits, followed by a zero bit.
110 110 0 0 0 0 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0
now, each procedure can store its delta against the
previous procedure (where the first procedure stores
its delta against a hypothetical zeroeth procedure of
token length 0 because it makes the math easier),
then, in next, we read a token, and then
scan through the dictionary to find that token. in
practice, we can do this a bit more efficiently.
because every token is strictly greater than the last,
which means that when a one bit is read, we can skip
all the tokens with a zero bit in that position.
001011 > 11 LINK
0 > 0 DELTA
0 > 0 DOCOL
011 > 3 DUP
001 > 1 +
100 > 4 EXIT
0000000 > [padding]
0011 > 3 LINK
0 > 0 DELTA
0 > 0 DOCOL
000 > 0 LIT
10000011 > 22 21
110 > 6 TWICE
010 > 2 .
101 > 5 BYE
00101100 01100110 00000000 00110000
01000001 11100101 01
now, we've reached 50 bits.
001011 > 11 LINK
0 > 0 DELTA
0 > 0 DOCOL
011 > 3 DUP
001 > 1 +
10 > 4 EXIT...
0 > ??? EXIT...LINK
11 > 2 ...LINK
0 > 0 DELTA
0 > 0 DOCOL
000 > 0 LIT
10000011 > 22 21
110 > 6 TWICE
010 > 2 .
101 > 5 BYE
00101100 01100110 01100000 10000011
11001010 1
41 bits. including the table, this time.
one thing that programmers are really bad at is trying
to guess how often their procedures are actually used.
the second thing programmers are really bad
at is trying to figure out when to extract repeated
code into a procedure.
this process is in fact called outlining, and isn't
applicable to our test program. however, in more
complicated programs, it can save a lot of space, and
make the code more readable at the same time. take
nip:
: drop t! ;
: swap t! >r t@ r> ;
: nip swap drop ;
for now, don't worry about those implementations of
swap and drop. the critical
issue occurs if every (or, nearly every)
usage of a procedure like nip is
immediately followed by another procedure or set of
procedures. if you think this can't happen, and you
program in c, name how many times you've used
memcmp without a ! before
it, and you'll get the point pretty fast.
nip is followed by a
procedure A, then we can just make a
procedure called nipA that does both at
once:
: drop t! ;
: swap t! >r t@ r> ;
: nipA swap drop A ;
so, what we can do is first inline all the
procedures of a program, and then very carefully
outline them optimally.
say we have a very inefficiently written procedure like this:
: foo bar baz bar bar baz bar ;
we begin with an empty hashmap from pairs of
procedures to a locations in the program. then, every
time we read a new pair of procedures, we try to add
it into the hashmap. if it doesn't exist, we just add
it and then move on. but if it already exists, then we
extract the pair into it's own procedure, then change
the program so that both previous occurances of the
pair use that procedure instead.
| pair being read | pairs discovered | new procedures | the current procedure |
|---|---|---|---|
| bar baz | : foo bar baz bar bar baz bar ; | ||
| baz bar | (bar baz) | : foo bar baz bar bar baz bar ; | |
| bar bar | (bar baz) (baz bar) | : foo _0 bar _0 bar ; | |
| bar baz | (bar baz) (baz bar) (bar bar) | : _0 bar baz ; | : foo _0 bar _0 bar ; |
| _0 bar | (_0 bar) | : _1 _0 bar ; | : foo _1 _1 ; |
: _0 bar baz ;
: _1 _0 bar ;
: foo _1 _1 ;
we then inline procedures that are only used once:
: _1 bar baz bar ;
: foo _1 _1 ;
simpleTM. now, we can use huffman threading
to compress that down, and we have our binary.
ah. that's. that's not good.
in forth, there are two pretty important procedures
for moving around elements on the stack:
r> and >r. these are
read "r from" and "to r", and either move an element
from the return stack to the data stack, or from the
data stack to the return stack, respectively.
the trouble is, if we begin inlining and outlining
procedures haphazardly, we might entirely change the
behaviour of a procedure, because invoking it adds a
new element to the return stack. so, actually we need
to keep those procedures outside of any weird inlining
or outlining shenanigans, unless they're
balanced, meaning that the procedure only
ever adds elements to the return stack and reads back
its own elements, not reading elements below or equal
to its own return address.
: foo t! >r t@ r> ; ( this is balanced! )
: bar r> t! ; ( this is not balanced. )
pretty simple. but we also can't break it up in any
way, i.e. this is no bueno:
: _0 t! >r ;
: foo _0 t@ r> ;
because _0 will actually jump to a random
location in memory and begin executing invalid code,
which, contrary to popular belief, is not the original
behaviour of the program.
[9]
the above all leads up to the description of
rontoforth, a compiler i've been trying to
extantize for the past few weeks.
we've looked at many different ways to encode our test
program, ranging from the original 384 bits all the
way down to 41. the reason why we can afford a
complicated next function is that our
next wouldn't change from program to
program. its complexity is O(1), meaning that as the
program gets twice as big, the next
function doesn't get any bigger. this is in opposition
to the actual program itself, where as it gets twice
as big, it gets... twice as big. if we can slow that
growth down even a little bit, it won't affect the
smaller programs that much, but it'll cut down the
larger programs by a significant amount.
we can keep optimizing the code again and again with
different methods and techniques, making more and more
assumptions about how programs are structured, but at
some point we'll hit a wall. take a simple program
that exits with code 0. the absolute smallest it can
possibly be on an amd64 linux machine is
mov al, 0x3c
syscall
which is four
bytes[10].
two of them have to be the
syscall instruction, because otherwise
the program can't talk to the operating system. and
the other two have to load 0x3c
into eax somehow, because otherwise it'll
tell the operating system to do something entirely
different, and there's no reliable value of
0x3c hanging around in our initial
environment anywhere in a way that we can load it in
with just one instruction, so it is what it is. with a
different operating system, like dos for instance, an
equivalent program is just one byte:
ret
because we can validly return from the program, and
that goes back to dos. in the linux case, returning
just causes the instruction pointer to go into west
hyperspace, which is not particularly good.
: and ;
here are, in fact, also procedures. they just
happen to execute at "compile time". the technical
term is an
immediate
word, looking into it will cause headache, source:
me.
[back]
: foo 2 ;
: foo foo 1 + ;
foo . ( 3 )
here, the redefinition of foo
refers to the previous definition.
: factorial dup 0= if drop 1 else dup 1- recurse * then ;however, rontoforth doesn't have
recurse, so we're good.
[back]